Дон Кнут работи по Том 4 на Изкуство на компютърното програмиране. Една от главите е за двоични диаграми на решенията и техните приложения, тема, която намирам за много интересна. Кнут показва, че множество интересни графични проблеми могат да бъдат кодирани като булеви формули, а полученото BDD представлява всички възможни решения на проблема. Често има някакъв критерий за оптимизация и е доста лесно да се извлече „най-доброто“ решение от BDD чрез прост алгоритъм за динамично програмиране. Тук ние показваме няколко примера, използвайки графиката, представяща 48 съседни състояния, с възел за всяко състояние, и ръб между две състояния, ако те споделят граница. За всяка от картите, ако кликнете върху изображението, ще стигнете до изходния документ във формат SVG. Ето графиката, разположена в главните региони на държавите:

Капиталови обиколки
Да предположим, че искате да посетите столицата на 48-те държави с изискването да преминавате само веднъж през всяка държава. (С други думи, искате да намерите Хамилтонова пътека в графиката.) Както можете да видите от горната карта, ако следвате най-прекия път между столиците на държавите, често ще преминавате през друга държава, или в случай на пътуване от Лансинг, Мичиган до Медисън, Уисконсин, ще карате през езерото Мичиган. Вместо това трябва да вземете най-краткия маршрут, който остава в двете състояния за всеки крак на пътуването. Нека да наречем такъв маршрут на Капитал обиколка. Ето диаграма на допустимите маршрути между държавите:

Въз основа на прост анализ, плюс усилията на Кнут, можем да кажем следното:
- Всички обиколки трябва да започнат или да завършат в Мейн, тъй като Мейн има само един съсед. Ще използваме Мейн като отправна точка.
- Всички обиколки трябва да свършат след Ню Йорк, тъй като това е точка на артикулация.
- Общо са 68,656,026 различни капиталови обиколки.
Тук е най-кратката обиколка на столицата, на обща стойност 11,698 мили:

Тук е най-дългата обиколка на столицата, на обща стойност 18,040 мили:

Оцветяване на графиката
Друг интересен клас проблеми включва оцветяване на картата. Правилото е, че няма две съседни държави, които да имат един и същи цвят. Известният Теорема за четири цвята заявява, че всяка равнинна графика може да бъде оцветена с най-много четири цвята.
Тъй като BDD кодира всички възможни решения на булева формула, лесно можем да изчислим колко решения има. За оцветяване на графика, ние коригираме броя на точките, за да елиминираме симетриите, дължащи се на произволното присвояване на цветови стойности (4! Симетрични случая за 4-оцветяване).
За оцветяване на съседни 48 състояния има 533,816,322,048 възможни оцветители. (Това е 1/2 от броя, докладван от Кнут, тъй като неговата карта включва Вашингтон като 49-то “състояние” и може да бъде назначен един от двата цвята, които не се използват за Мериленд и Вирджиния.) Ето някои интересни примери за специални оцветители:
- Балансиран оцветител, в който всеки цвят се използва точно за 12 държави. Има 12,554,677,864 такива оцветители, което е изненадващо високо 2,4% от всички възможни оцветители.
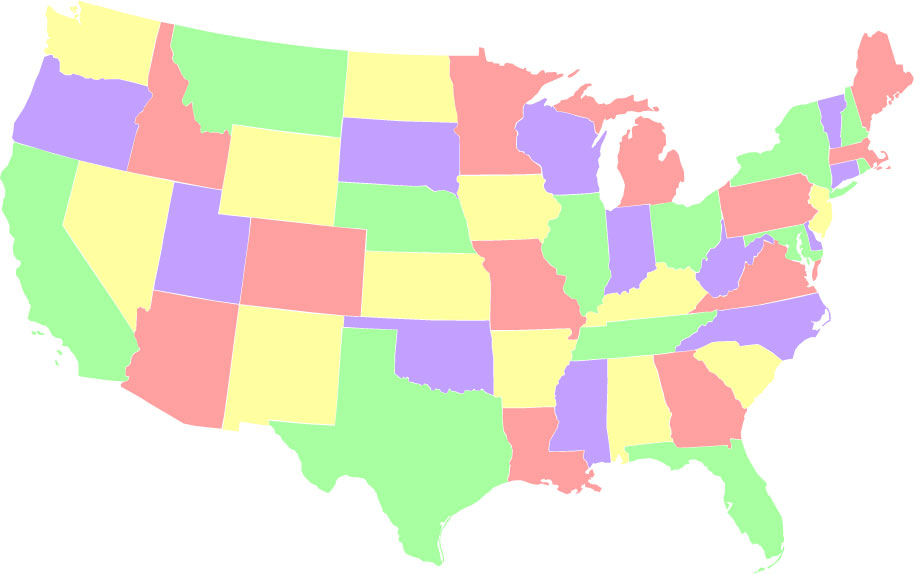
- Небалансирано оцветяване, при което един от цветовете (зелен) се използва възможно най-малко (2 състояния). Има само 288 начина за оцветяване на картата, така че един цвят да се използва само два пъти.

- Небалансирано оцветяване, при което един от цветовете (жълт) се използва колкото е възможно повече (18 държави). Има 71,002,368 начина за оцветяване на картата, така че един цвят да се използва 18 пъти.
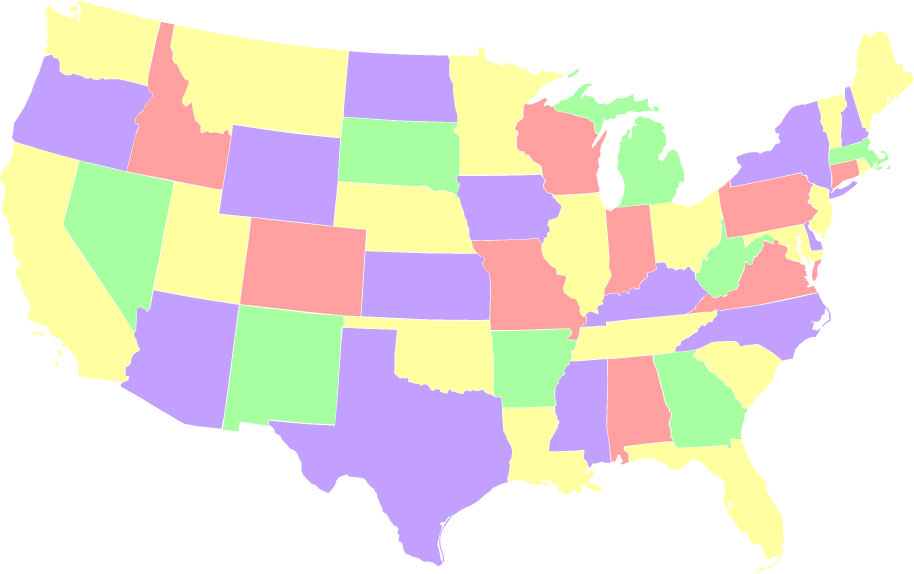
- Комбинирането на двете. Оцветители, използващи цветовете 2, 13, 15 и 18 пъти. Тази последователност 1) отляво надясно, използва всеки цвят последователно за най-малко възможен брой пъти и 2) от дясно на ляво, използва всеки цвят последователно за възможно най-много пъти. Има 24 такива решения.

От гледна точка на програмите за оцветяване на графиките, картата на щатите 48 в САЩ е доста проста. За по-сложна карта, вижте уеб страницата на Графика на Макгрегър.
Translated by Aleksandar Damyan
Read the original page here.
